martes, 7 de junio de 2011

combinacion lineal!!!!!!

Combinación lineal

Un vector \ x se dice que es combinación lineal de un conjunto de vectores \ A = \{ x_1, x_2, x_3,...,x_n \}\in (V,\mathbb{K}) si existe una forma de expresarlo como suma de parte o todos los vectores de \ A multiplicados cada uno de ellos por un coeficiente escalar \ a_1, a_2, ..., a_n \in \mathbb{K}, de forma que:
\ x = a_1 x_1 + a_2 x_2 + ... + a_n x_n = \sum_{i=1}^n a_i x_i.
Así, \ x es combinación lineal de vectores de \ A si podemos expresar \ x como una suma de múltiplos de una cantidad finita de elementos de \ A.
Ejemplo: 2x + 3y − 2z = 0. Se dice que z es combinación lineal de x y de y, porque podemos escribir z = x + \frac{3}{2} y sin más que despejar la z. De la misma manera, despejando oportunamente, cada una de estas variables se podría expresar como combinación lineal de las otras dos.
En otras palabras, cuánto de cada vector del conjunto \ A necesito para que, cuando se combinen linealmente dichos elementos , pueda formar al vector \ x en cuestión.



Publicado por genesis,karla,joselin en 17:47 0 comentarios

sume algebraica de los vectores!!!!!

Las propiedades que cumple la suma de vectores son las misma que cumplían las estructuras algebraica de una operación que son: la de cierre, la conmutativa, la asociativa, elemento neutro e identidad y la distributiva.

ESTRUCTURAS ALGEBRAICAS
Una estructura algebraica es un conjunto de operaciones binarias, esta se representan <A, operación>, <{a, b, c}, operación>, así se representan las estructuras algebraicas sencillas, las dobles se representan <conjunto, 1o. operación, 2o. operación>.

Publicado por genesis,karla,joselin en 17:40 0 comentarios

vectores equipolentes!!!!

Decimos que dos o más vectores son equipolentes cuando las mágnitudes físicas que representan tienen el mismo valor y producen los mismos efectos.

Archivo:Moglfm0101 equipolencia.jpg
Publicado por genesis,karla,joselin en 17:28 0 comentarios

vectores en el plano!!!!!!!

En un sistema de ejes cartesianos, cada punto se describe mediante sus coordenadas.
Mueve el punto A para que sus coordenadas sean A(-2,1).

Dados los puntos A y B, la flecha que va de A a B se llama vector, se representa por . A es el origen del vector y B el extremo.
Para calcular las coordenadas del vector AB, se restan las coordenadas del extremo menos las del origen.
Si el origen del vector es el origen de coordenadas (0,0), las coordenadas del extremo son las coordenadas del vector.

Publicado por genesis,karla,joselin en 17:22 0 comentarios

miércoles, 6 de abril de 2011

Trigonometría

Trigonometria 02.svg
La trigonometría es una rama de la matemática, cuyo significado es "la medición de los triángulos".

Las funciones trigonométricas
 
La trigonometría como rama de las matemáticas realiza su estudio en la relación entre los lados y ángulos de un triángulo rectángulo, con una aplicación inmediata en geometría y sus aplicaciones. Para el desarrollo de este fin se definieron una serie de funciones que han sobrepasado su fin original, convirtiéndose en elementos matemáticos estudiados en sí mismos y con aplicaciones en los campos más diversos.

 Razones trigonométricas

Trigono b00.svg
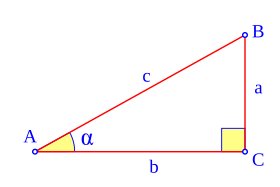
El triángulo ABC es un triángulo rectángulo en C; lo usaremos para definir las razones seno, coseno y tangente, del ángulo 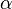\alpha \, , correspondiente al vértice A, situado en el centro de la circunferencia.
  • El seno (abreviado como sen, o sin por llamarse "senos" en latín) es la razón entre el cateto opuesto sobre la hipotenusa,
\operatorname {sen} \, \alpha = \frac{\overline{CB}}{\overline{AB}} = \frac{a}{c}
  • El coseno (abreviado como cos) es la razón entre el cateto adyacente sobre la hipotenusa,
\cos\alpha = \frac{\overline{AC}}{\overline{AB}} = \frac{b}{c}
  • La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto sobre el cateto adyacente,
\tan\alpha = \frac{\overline{CB}}{\overline{AC}} = \frac{a}{b}

 Razones trigonométricas recíprocas

Trigono d00.svg
  • La Cosecante: (abreviado como csc o cosec) es la razón recíproca de seno, o también su inverso multiplicativo:
\csc \alpha = \frac{1}{\operatorname {sen} \; \alpha} = \frac{c}{a}
En el esquema su representación geométrica es:
\csc \alpha = \overline{AG}
  • La Secante: (abreviado como sec) es la razón recíproca de coseno, o también su inverso multiplicativo:
\sec \alpha = \frac{1}{\operatorname {cos} \; \alpha} = \frac{c}{b}
En el esquema su representación geométrica es:
\sec \alpha = \overline{AD}
  • La Cotangente: (abreviado como cot o cta) es la razón recíproca de la tangente, o también su inverso multiplicativo:
\cot \alpha = \frac{1}{\tan \alpha} = \frac{b}{a}
En el esquema su representación geométrica es:
\cot \alpha = \overline{GF}
Normalmente se emplean las relaciones trigonométricas seno, coseno y tangente, y salvo que haya un interés específico en hablar de ellos o las expresiones matemáticas se simplifiquen mucho, los términos cosecante, secante y cotangente no suelen utilizarse.

 Otras funciones trigonométricas

Además de las funciones anteriores existen otras funciones trigonométricas, matemáticamente se pueden definir empleando las ya vistas, su uso no es muy corriente, pero si se emplean dado su sentido geométrico, veamos:
El seno cardinal o función sinc (x) definida:
\operatorname {sinc} \; (x) = \frac{\sin(x)}{x}
El verseno, es la distancia que hay entre la cuerda y el arco en una circunferencia, también se denomina sagita o flecha, se define:
\operatorname {versen} \; \alpha = 1 - \cos \alpha
El semiverseno, se utiliza en navegación al intervenir en el cálculo esférico:
\operatorname {semiversen} \; \alpha = \frac {\operatorname {versen} \; \alpha }{2}
El coverseno,
\operatorname {coversen} \; \alpha = 1 - \operatorname {sen} \; \alpha
El semicoverseno
\operatorname {semicoversen} \; \alpha = \frac { \operatorname {coversen} \; \alpha }{2}
El exsecante:
\operatorname {exsec} \; \alpha = \sec \alpha - 1

 Funciones trigonométricas inversas

En trigonometría, cuando el ángulo se expresa en radianes (dado que un radián es el arco de circunferencia de longitud igual al radio), suele denominarse arco a cualquier cantidad expresada en radianes; por eso las funciones inversas se denominan con el prefijo arco,
y= \operatorname {sen} \, x \,
y es igual al seno de x, la función inversa:
x = \operatorname {arcsen} \; y \,
x es el arco cuyo seno vale y, o también x es el arcoseno de y.
si:
y= \cos x \,
y es igual al coseno de x, la función inversa:
x = \arccos y \,
x es el arco cuyo coseno vale y, que se dice: x es el arcocoseno de y.
si:
y= \tan x \,
y es igual al tangente de x, la función inversa:
x = \arctan y \,
x es el arco cuya tangente vale y, o x es igual al arcotangente de y.Identidades trigonométricas
Artículo principal: Identidades trigonométricas
Una identidad es una igualdad en que se cumple para todos los valores permisibles de la variable. En trigonometría existen seis identidades fundamentales:

 Recíprocas

\operatorname {sen} (\alpha) \cdot \csc (\alpha) = 1
\operatorname {cos} (\alpha) \cdot \sec (\alpha) = 1
\operatorname {tan} (\alpha) \cdot \cot (\alpha) = 1

 De división

Trigono a00.svg
\tan (\alpha) = \frac {\operatorname {sen} (\alpha)}{ \cos (\alpha)}

 Por el teorema de Pitágoras

Como en el triángulo rectángulo cumple la función que:
a^2 + b^2 = c^2 \,
de la figura anterior se tiene que:
\operatorname {sen} (\alpha ) = \frac {a}{c}
cos (\alpha ) = \frac {b}{c}
por tanto:
\operatorname {sen}^2 \alpha + \cos^2 \alpha = \bigg(\dfrac {a}{c}\bigg) ^2 + \bigg(\frac {b}{c}\bigg)^2 = \frac {a^2 + b^2 }{c^2} = \frac {c^2}{c^2} = 1
entonces para todo ángulo α, se cumple la identidad Pitagórica:
\operatorname {sen}^2 \alpha + \cos^2 \alpha = 1 \,
que también puede expresarse:
\tan^2 \alpha + 1 = \sec^2 \alpha \,
1+\cot^2 \alpha = \csc^2 \alpha \,

 Suma y diferencia de dos ángulos

\operatorname {sen}(\alpha + \beta) = \operatorname {sen} \alpha \cos \beta + \cos \alpha \operatorname {sen} \beta \,

\operatorname {sen}(\alpha - \beta) = \operatorname {sen} \alpha \cos \beta - \cos \alpha \operatorname {sen} \beta \,

\cos(\alpha + \beta) = \cos \alpha \cos \beta - \operatorname {sen} \alpha \operatorname {sen} \beta \,

\cos(\alpha - \beta) = \cos \alpha \cos \beta + \operatorname {sen} \alpha \operatorname {sen} \beta \,

\begin{align} & {\mathrm{\vdash}\cos{\mathrm{(}}{x}\mathrm{{-}}{y}{\mathrm{)}}\mathrm{{=}}\cos{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\cos{\mathrm{(}}{y}{\mathrm{)}}\mathrm{{+}}\sin{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\sin{\mathrm{(}}{y}{\mathrm{)}}}\\ & {}\\ & {{i}{\mathrm{)}}{Se}\;{parte}\;{de}{\mathrm{:}}}\\ & {}\\ & {\sin{\mathrm{(}}{x}\mathrm{{-}}{y}{\mathrm{)}}\mathrm{{=}}\sin{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\cos{\mathrm{(}}{y}{\mathrm{)}}\mathrm{{-}}\cos{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\sin{\mathrm{(}}{y}{\mathrm{)}}}\\ & {}\\ & {{ii}{\mathrm{)}}{Se}\;{deriva}\;{la}\;{igualdad}{\mathrm{,}}\;{entonces}{\mathrm{:}}}\\ & {}\\ & {\frac{d}{dx}\sin{\mathrm{(}}{x}\mathrm{{-}}{y}{\mathrm{)}}\mathrm{{=}}\frac{d}{dx}\sin{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\cos{\mathrm{(}}{y}{\mathrm{)}}\mathrm{{-}}\frac{d}{dx}\cos{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\sin{\mathrm{(}}{y}{\mathrm{)}}}\\ & {}\\ & {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{{=}}\cos{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\cos{\mathrm{(}}{y}{\mathrm{)}}\mathrm{{-}}{\mathrm{(}}\mathrm{{-}}\sin{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\sin{\mathrm{(}}{y}{\mathrm{))}}}\\ & {}\\ & {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{{=}}\cos{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\cos{\mathrm{(}}{y}{\mathrm{)}}\mathrm{{+}}\sin{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\sin{\mathrm{(}}{y}{\mathrm{)}}}\\ & {}\\ & {\mathrm{\therefore}\;{queda}\;{demostrada}\;{la}\;{igualdad}{\mathrm{.}}}\\ & {} \end{align}

\tan(\alpha + \beta) = \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta}

\tan(\alpha - \beta) = \frac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta}

 Suma y diferencia del seno y coseno de dos ángulos

\operatorname {sen} \alpha + \operatorname {sen} \beta = 2\operatorname {sen} \left( \frac{\alpha + \beta}{2}\right)\cos \left(\frac{\alpha - \beta}{2} \right)

\operatorname {sen} \alpha - \operatorname {sen} \beta = 2\operatorname {sen} \left( \frac{\alpha - \beta}{2}\right)\cos \left(\frac{\alpha + \beta}{2} \right)

\cos \alpha + \cos \beta = 2\cos \left(\frac{\alpha + \beta}{2} \right)\cos \left(\frac{\alpha - \beta}{2}\right)

\cos \alpha - \cos \beta = -2\operatorname {sen} \left(\frac{\alpha + \beta}{2} \right) \operatorname {sen} \left(\frac{\alpha - \beta}{2}\right)

 Producto del seno y coseno de dos ángulos

\cos(\alpha) \cos(\beta) = \frac{\cos(\alpha + \beta) + \cos(\alpha - \beta) }{ 2}
\operatorname {sen}(\alpha) \operatorname {sen}(\beta) = \frac{\cos(\alpha - \beta) - \cos(\alpha + \beta) }{ 2}
\operatorname {sen}(\alpha) \cos(\beta) = \frac{\operatorname {sen}(\alpha + \beta) + \operatorname {sen}(\alpha - \beta) }{ 2}
\cos(\alpha) \operatorname {sen}(\beta) = \frac{\operatorname {sen}(\alpha + \beta) - \operatorname {sen}(\alpha - \beta) }{ 2}

 Ángulo doble

\operatorname {sen} 2\alpha = 2 \operatorname {sen}\alpha \cdot \cos \alpha \,\!

\cos 2\alpha = \cos^2 \alpha - \operatorname {sen}^2 \alpha \,\!

\cos 2\alpha = 1 - 2 \operatorname {sen}^2 \alpha \,\!

\cos 2\alpha = -1 + 2 \cos^2 \alpha \,\!

\tan 2\alpha = \frac{2\tan \alpha}{1 - \tan^2 \alpha}

\operatorname {sen}^2 \alpha = \frac{1-\cos 2\alpha}{2}

\cos^2 \alpha = \frac{1+\cos 2\alpha}{2}

 Ángulo mitad

\operatorname {sen}\left(\frac{\alpha}{2} \right) = \sqrt{\frac{1-\cos\alpha}{2}} \,\!

\cos \left(\frac{\alpha}{2} \right) = \sqrt{\frac{1+\cos\alpha}{2}} \,\!

\tan \left(\frac{\alpha}{2} \right) = \sqrt{\frac{1-\cos\alpha}{1+\cos\alpha}}

\begin{align} & {\mathrm{\vdash}\tan{\mathrm{(}}\frac{u}{2}{\mathrm{)}}\mathrm{{=}}\frac{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}{\sin\mathrm{(}u\mathrm{)}}}\\ & {}\\ & {{i}{\mathrm{)}}\;{Se}\;{parte}\;{de}\;\tan{\mathrm{(}}{x}{\mathrm{)}}\mathrm{{=}}\frac{\sin\mathrm{(}x\mathrm{)}}{\cos\mathrm{(}x\mathrm{)}}{\mathrm{,}}\;{entonces}{\mathrm{:}}}\\ & {}\\ & {\tan{\mathrm{(}}\frac{u}{2}{\mathrm{)}}\mathrm{{=}}\frac{\sqrt{\frac{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}{2}}}{\sqrt{\frac{{1}\mathrm{{+}}\cos{\mathrm{(}}{u}{\mathrm{)}}}{2}}}}\\ & {}\\ & {{ii}{\mathrm{)}}\;{Se}\;{multiplica}\;{por}\;{uno}\;{para}\;{\mathrm{eliminar}}\;{las}\;{raices}\;{de}\;{dos}{\mathrm{:}}}\\ & {}\\ & {\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{{=}}\frac{\sqrt{2}}{\sqrt{2}}\mathrm{\cdot}\frac{\mathrm{(}\tfrac{\sqrt{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}}{\sqrt{2}}\mathrm{)}}{\mathrm{(}\tfrac{\sqrt{{1}\mathrm{{+}}\cos{\mathrm{(}}{u}{\mathrm{)}}}}{\sqrt{2}}\mathrm{)}}}\\ & {}\\ & {\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{{=}}\frac{\sqrt{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}}{\sqrt{{1}\mathrm{{+}}\cos{\mathrm{(}}{u}{\mathrm{)}}}}}\\ & {}\\ & {{iii}{\mathrm{)}}\;{Se}\;{multiplica}\;{otra}\;{vez}\;{por}\;{un}\;{uno}\;{para}\;{obtener}{\mathrm{:}}}\\ & {}\\ & {\tan{\mathrm{(}}\frac{u}{2}{\mathrm{)}}\mathrm{{=}}\sqrt{\frac{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}{{1}\mathrm{{+}}\cos{\mathrm{(}}{u}{\mathrm{)}}}}\mathrm{\cdot}\sqrt{\frac{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}}}\\ & {}\\ & {\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{{=}}\sqrt{\frac{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}{{1}\mathrm{{+}}\cos{\mathrm{(}}{u}{\mathrm{)}}}\mathrm{\cdot}\frac{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}}}\\ & {}\\ & {\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{{=}}\sqrt{\frac{{\mathrm{(}}{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{))}}^{2}}{{1}\mathrm{{-}}{\cos}^{2}{\mathrm{(}}{u}{\mathrm{)}}}}}\\ & {}\\ & {{iv}{\mathrm{)}}\;{Utilizando}\;{sen}^{2}{x}\mathrm{{=}}{1}\mathrm{{-}}{\cos}^{2}{x}{\mathrm{,}}\;{se}\;{obtiene}{\mathrm{:}}}\\ & {}\\ & {\tan{\mathrm{(}}\frac{u}{2}{\mathrm{)}}\mathrm{{=}}\frac{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}{\sqrt{{\sin}^{2}\mathrm{(}u\mathrm{)}}}}\\ & {}\\ & {\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{{=}}\frac{{1}\mathrm{{-}}\cos{\mathrm{(}}{u}{\mathrm{)}}}{\sin\mathrm{(}u\mathrm{)}}}\\ & {}\\ & {\mathrm{\therefore}\;{La}\;{igualdad}\;{queda}\;{demostrada}{\mathrm{.}}} \end{align}

Otras identidades trigonométricas

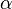\operatorname {sen} \left ( \frac{\pi}{2} - \alpha \right ) = \cos \alpha \,\!
\cos \left ( \frac{\pi}{2} - \alpha \right ) = \operatorname {sen}\alpha \,\!
\operatorname {sen} (\pi - \alpha) = \operatorname {sen}\alpha \,\!
\cos (\pi - \alpha) = - \cos \alpha \,\!
\operatorname {sen} (2\pi - \alpha) = - \operatorname {sen} \alpha \,\!
\cos (2\pi - \alpha) = \cos \alpha \,\!
\operatorname {sen}\alpha \cdot \cos \alpha + \operatorname {sen}\beta \cdot \cos \beta = \operatorname {sen}(\alpha + \beta) \cdot \cos(\alpha - \beta)
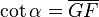
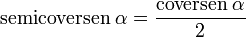
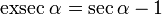
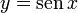
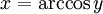
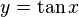
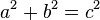
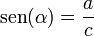
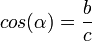
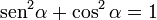
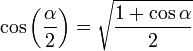
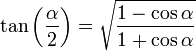
\begin{align} & {\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{)}}\mathrm{{+}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{)}}\mathrm{{=}}\arcsin{\mathrm{[}}\mathit{\alpha}\sqrt{{1}\mathrm{{-}}{\mathit{\beta}}^{2}}\mathrm{{+}}\mathit{\beta}\sqrt{{1}\mathrm{{-}}{\mathit{\alpha}}^{2}}}\\ & {}\\ & {\mathrm{\vdash}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{)}}\mathrm{{+}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{)}}\mathrm{{=}}\arcsin{\mathrm{[}}\mathit{\alpha}\sqrt{{1}\mathrm{{-}}{\mathit{\beta}}^{2}}\mathrm{{+}}\mathit{\beta}\sqrt{{1}\mathrm{{-}}{\mathit{\alpha}}^{2}}}\\ & {}\\ & {{i}{\mathrm{)}}\;{Usando}\;{cambio}\;{de}\;{variables}\;{tenemos}\;{que}{\mathrm{:}}}\\ & {}\\ & {{x}\mathrm{{=}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{)}}}\\ & {}\\ & {{y}\mathrm{{=}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{)}}}\\ & {}\\ & {{ii}{\mathrm{.}}{i}{\mathrm{)}}{Se}\;{opera}\;{con}\;{el}\;\sin{\mathrm{(}}{x}\mathrm{{+}}{y}{\mathrm{),}}\;{entonces}{\mathrm{:}}}\\ & {}\\ & {\sin{\mathrm{(}}{x}\mathrm{{+}}{y}{\mathrm{)}}\mathrm{{=}}\sin{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\cos{\mathrm{(}}{y}{\mathrm{)}}\mathrm{{+}}\cos{\mathrm{(}}{x}{\mathrm{)}}\mathrm{\cdot}\sin{\mathrm{(}}{y}{\mathrm{)}}}\\ & {}\\ & {{iii}{\mathrm{.}}{i}{\mathrm{)}}{Se}\;{obtiene}\;{el}\;{equivalente}\;{del}\;\cos{\mathrm{(}}{x}{\mathrm{):}}}\\ & {}\\ & {{\cos}^{2}{\mathrm{(}}{x}{\mathrm{)}}\mathrm{{+}}{\sin}^{2}{\mathrm{(}}{x}{\mathrm{)}}\mathrm{{=}}{1}}\\ & {}\\ & {{\cos}^{2}{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{))}}\mathrm{{=}}{1}\mathrm{{-}}{\sin}^{2}{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{))}}}\\ & {}\\ & {{\cos}^{2}{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{))}}\mathrm{{=}}{1}\mathrm{{-}}{\mathrm{[}}\sin{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{))}}\mathrm{\cdot}\sin{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{))]}}}\\ & {}\\ & {{\cos}^{2}{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{))}}\mathrm{{=}}{1}\mathrm{{-}}{\mathrm{(}}\mathit{\alpha}\mathrm{\cdot}\mathit{\alpha}{\mathrm{)}}}\\ & {}\\ & {\cos{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{))}}\mathrm{{=}}\sqrt{{1}\mathrm{{-}}{\mathit{\alpha}}^{2}}}\\ & {}\\ & {{iii}{\mathrm{.}}{ii}{\mathrm{)}}\;{Se}\;{obtiene}\;{el}\;{equivalente}\;{de}\;\cos{\mathrm{(}}{y}{\mathrm{)}}\;{\mathrm{:}}}\\ & {}\\ & {{\cos}^{2}{\mathrm{(}}{y}{\mathrm{)}}\mathrm{{+}}{\sin}^{2}{\mathrm{(}}{y}{\mathrm{)}}\mathrm{{=}}{1}}\\ & {}\\ & {{\cos}^{2}{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))}}\mathrm{{=}}{1}\mathrm{{-}}{\sin}^{2}{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))}}}\\ & {}\\ & {{\cos}^{2}{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))}}\mathrm{{=}}{1}\mathrm{{-}}{\mathrm{[}}\sin{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))}}\mathrm{\cdot}\sin{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))]}}}\\ & {}\\ & {{\cos}^{2}{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))}}\mathrm{{=}}{1}\mathrm{{-}}{\mathrm{(}}\mathit{\beta}\mathrm{\cdot}\mathit{\beta}{\mathrm{)}}}\\ & {}\\ & {\cos{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))}}\mathrm{{=}}\sqrt{{1}\mathrm{{-}}{\mathit{\beta}}^{2}}}\\ & {}\\ & {{ii}{\mathrm{.}}{ii}{\mathrm{)}}{Se}\;{sustituyen}\;{del}\;{paso}\;{iii}{\mathrm{)}}\;{el}\;\cos{\mathrm{(}}{x}{\mathrm{)}}\;{y}\;{el}\;\cos\;{\mathrm{(}}{y}{\mathrm{):}}}\\ & {}\\ & {\sin{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{)}}\mathrm{{+}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))}}\mathrm{{=}}{\mathrm{\{[}}\sin{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{))]}}\mathrm{\cdot}{\mathrm{(}}\sqrt{{1}\mathrm{{-}}{\mathit{\beta}}^{2}}{\mathrm{)\}}}\mathrm{{+}}{\mathrm{\{(}}\sqrt{{1}\mathrm{{-}}{\mathit{\alpha}}^{2}}{\mathrm{)}}\mathrm{\cdot}{\mathrm{[}}\sin{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))]\}}}}\\ & {}\\ & {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathrm{{=}}{\mathrm{[}}\mathit{\alpha}\mathrm{\cdot}\sqrt{{1}\mathrm{{-}}{\mathit{\beta}}^{2}}{\mathrm{]}}\mathrm{{+}}{\mathrm{[}}\mathit{\beta}\mathrm{\cdot}\sqrt{{1}\mathrm{{-}}{\mathit{\alpha}}^{2}}{\mathrm{]}}}\\ & {}\\ & {{iv}{\mathrm{)}}{Se}\;{obtiene}\;{el}\;\arcsin{\mathrm{[}}\sin{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{)}}\mathrm{{+}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))],}}\;{para}\;{te}{\mathrm{rmin}}{ar}\;{la}\;{demostracion}{\mathrm{:}}}\\ & {}\\ & {\arcsin{\mathrm{[}}\sin{\mathrm{(}}\arcsin{\mathrm{(}}\mathit{\alpha}{\mathrm{)}}\mathrm{{+}}\arcsin{\mathrm{(}}\mathit{\beta}{\mathrm{))]}}\mathrm{{=}}\;\arcsin{\mathrm{[}}\mathit{\alpha}\mathrm{\cdot}\sqrt{{1}\mathrm{{-}}{\mathit{\beta}}^{2}}\mathrm{{+}}\mathit{\beta}\mathrm{\cdot}\sqrt{{1}\mathrm{{-}}{\mathit{\alpha}}^{2}}{\mathrm{]}}}\\ & {}\\ & {\mathrm{\therefore}\;{queda}\;{demostrada}\;{la}\;{igualdad}{\mathrm{.}}} \end{align}
 

Publicado por genesis,karla,joselin en 20:06 0 comentarios